## 编码
合法华容道均有编码,长度9位,每一位是单个16进制数(0\~9与A\~F);同一布局只能有唯一编码,同一编码亦对应唯一布局,即编码与布局一一对应;
**位置编号**

2 x 2棋子的左上角在棋盘中的位置编号有12种情况,对应编码分别为:0、1、2、4、5、6、8、9、A(10)、C(12)、D(13)、E(14),将其置于编码第一位;剩余8位十六进制位储存其他棋子信息。
其余棋子(空格此时暂时视为棋子)按从左到右,从上到下的顺序排列(取左上角排序)
它们对应的代号(二进制)如下:
| 棋子类型 | 代号 |
| :-: | :-: |
| 空格 | 00 |
| 2 x 1 | 01 |
| 1 x 2 | 10 |
| 1 x 1 | 11 |
十六进制可按位转为二进制,对应关系如下:
| 十六进制 | 二进制 | 十进制 |
| :-: | :-: | :-: |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| A | 1010 | 10 |
| B | 1011 | 11 |
| C | 1100 | 12 |
| D | 1101 | 13 |
| E | 1110 | 14 |
| F | 1111 | 15 |
8个十六进制位相当于32个二进制位,由于每个棋子占用2个二进制位,因此最多储存16个棋子信息;将其依次填入,若有空余则补0填;按此操作即可将布局转化为编码,规定编码最后的0可以省略。
## 编码举例
**例1:**
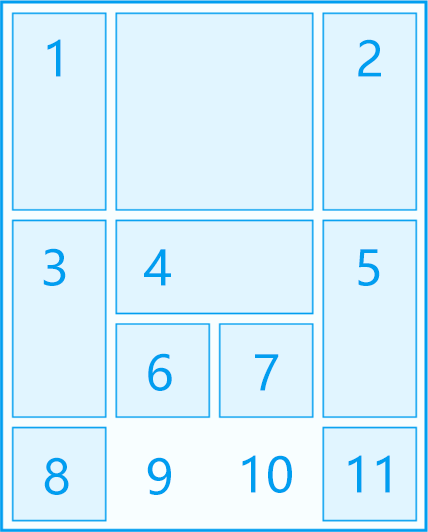
| 2 x 2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
补0 |
| 0001 |
10 |
10 |
10 |
01 |
10 |
11 |
11 |
11 |
00 |
00 |
11 |
00 |
00 |
00 |
00 |
00 |
| 1 |
A |
9 |
B |
F |
0 |
C |
0 |
0 |
因此,布局编码为1A9BF0C00,可简写为1A9BF0C
**例2:**

| 2 x 2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
补0 |
| 0100 |
11 |
11 |
11 |
10 |
10 |
10 |
00 |
01 |
00 |
11 |
01 |
00 |
00 |
00 |
00 |
00 |
| 4 |
F |
E |
A |
1 |
3 |
4 |
0 |
0 |
因此,布局编码为4FEA13400,可简写为4FEA134
**例3:**
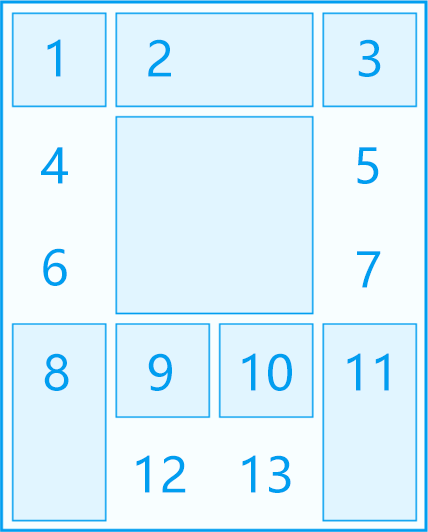
| 2 x 2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
补0 |
| 0101 |
11 |
01 |
11 |
00 |
00 |
00 |
00 |
10 |
11 |
11 |
10 |
00 |
00 |
00 |
00 |
00 |
| 5 |
D |
C |
0 |
2 |
F |
8 |
0 |
0 |
因此,布局编码为5DC02F800,可简写为5DC02F8