8.9 KiB
华容道布局
合法布局定义
-
棋盘大小为4 x 5
-
棋子为2 x 2,2 x 1(1 x 2),1 x 1三种
-
棋子间不能重叠,且至少存在两个空格
-
有且仅有一个2 x 2块,其他类型不限定
(合法的布局必须满足以上四点)
合法华容道布局共有29334498种
标准情况与非标准情况
标准布局:存在5个2 x 1(或1 x 2)和4个1 x 1棋子的合法华容道布局(363480种)
非标准布局:除标准布局外的全部合法华容道布局(28971018种)
合法布局举例:
非法布局举例:
错误原因:
-
缺少2 x 2块
-
仅有一个空格
-
存在两个2 x 2块
-
存在3 x 1块
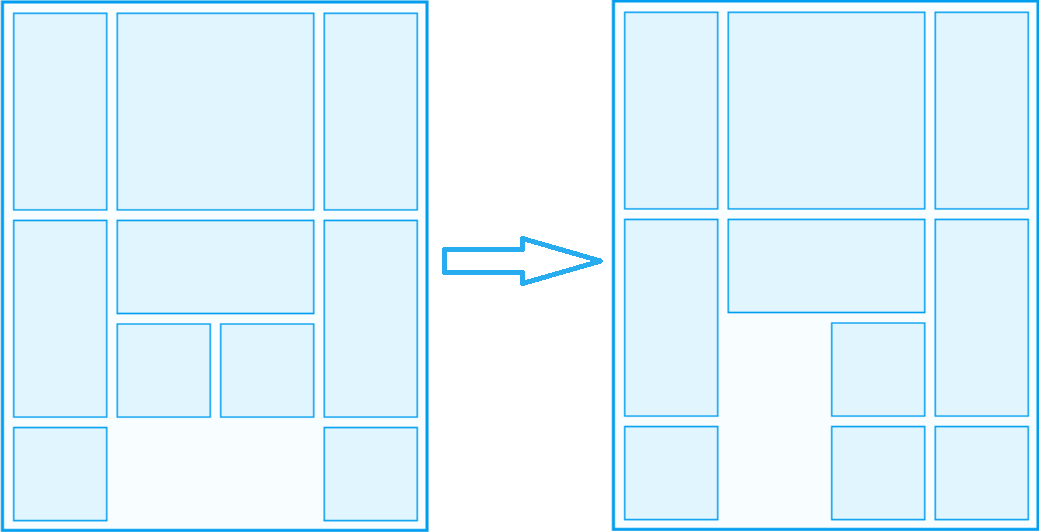
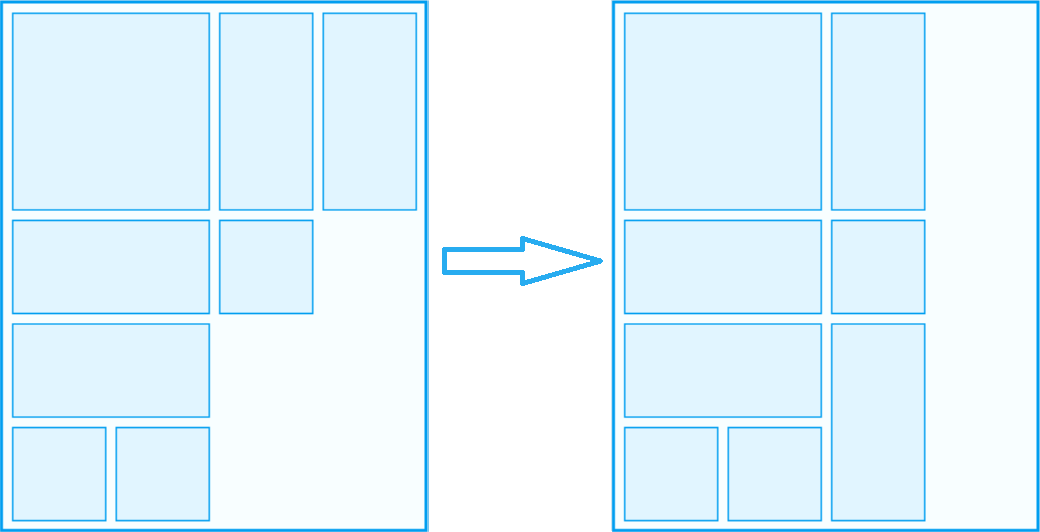
棋子移动
-
移动原则:棋子只能平行移动,不能进行旋转,移动后棋子间不可重叠;
-
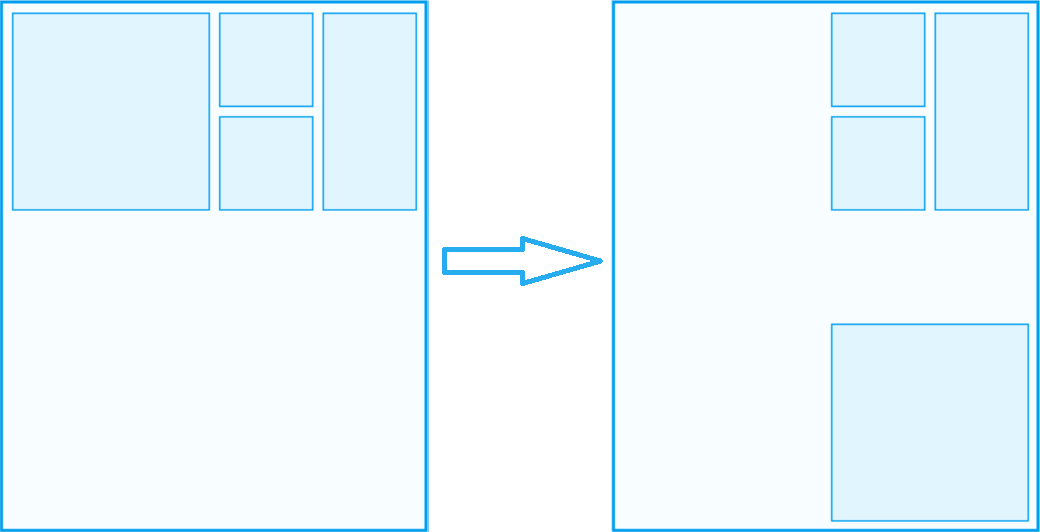
一步:某一棋子做任意次移动的过程;
-
子布局:某一布局通过一步移动得到的布局称为子布局;
-
相邻布局:两布局互为对方子布局时,两者为相邻布局;
性质:若布局A是布局B的子布局,则同时必有布局B是布局A的子布局;
步的举例
群
定义:群是有限个不同布局的集合,该集合中全部布局都可以由其中任一布局经过有限次移动得到;
性质1:群中任意一个布局无论如何移动,其结果仍在该群内;
性质2:只需群中任意一个布局,即可复原出群中的所有元素;
性质3:群是封闭的,群中所有元素无序且互异,同时构成一个关系网;
统计:29334498种布局可拆分出25422个群,其中元素数量存在两极分化现象;
群的种子
定义:群中任意一个布局称为该群的种子;
由上文性质2可知,群中任一布局进过多次移动可复原出整个群,故描述一个群仅需其中一个布局,常取其中编码最小的布局进行记录;
分类
布局id
合法布局共有29334498种,将它们从小到大排列,进而得到唯一的id(0 ~ 29334497);
摆列方式分类
2 x 1 与 1 x 2的数量
将2 x 1(1 x 2)的数量称为jiang_num;
由于至少存在两个空格,于是有0 ≤ jiang_num ≤ 7
可分为七种情况:
| jiang_num | COUNT |
|---|---|
| 0 | 786228 |
| 1 | 4190464 |
| 2 | 8729454 |
| 3 | 9090662 |
| 4 | 4995328 |
| 5 | 1381224 |
| 6 | 157630 |
| 7 | 3508 |
1 x 1块的数量
将1 x 1的数量称为bing_num,结合jiang_num进行分类;
由于至少存在两个空格,于是有0 ≤ bing_num ≤ (14 - jiang_num * 2)
据此可分为64种情况:
2 x 1与1 x 2块的方向
进而,将2 x 1块的数量称为style_num,则1 x 2块的数量为(jiang_num - style_num),于是有0 ≤ style_num ≤ jiang_num
此时可分出203种情况:
(注意不存在 jiang_num-bing_num-style_num = 7-0-0 ,即七竖将的情况)
按群继续分类
对于一个特定的 jiang_num-bing_num-style_num 分组,可拆分出n个群;将分出的群按元素数量从大到小排列,若存在元素数量相同的群,则取其中的最小元素排序;对这些群进行编号得0 ~ (n - 1) 共n个群,编号记为group_num;
因而对于某一群,存在一个唯一编号 jiang_num-bing_num-style_num-group_num ;由于群中的元素个数是确定的,将其中的元素按编码从小到大排列,其中的元素可得唯一编号group_index;
所以,对于任意布局,可得唯一编号 jiang_num-bing_num-style_num-group_num-group_index;
基本参数定义
最少步数:布局A和布局B处于同一个群,从布局A移动到B所需最少的步数,该数值存在且是确定的;
性质1:布局A到B的最少步数与布局B到A的最少步数必定相同;
性质2:若两布局不在同一个群中,则最少步数不存在;
最短路径:从布局A到布局B,所有满足最少步数的路径;
性质:最短路径在大多数情况下不止一条,且它们之间会相互交错,一般绘制多点层级路线图进行研究;
最远步数:布局A到它所在群中任一布局均存在一最少步数n,其中最大的n称为最远步数;
性质:标准华容道中不存在最远布局退化的情况,即最远步数至小为1;
最远布局:布局A到布局B的最少步数为最远步数时,称布局B为布局A的最远布局;
性质:最远布局必然存在,且大多数情况下不止一个;
下称满足2 x 2方块在棋盘的最下方中间的布局拥有特征S(即2 x 2块所在位置编号为13,亦或编码以D开头);
布局无解:布局A所在群中不存在满足特征S的布局;
解:布局A所在的群中存在布局T满足特征S,且布局A到T的任何最短路径上不存在满足特征S的节点,则称布局T为A的一个解;
最少步解的步数:若布局存在解,布局A到解的最少步数为n,其中最小的n称为最少步解的步数;
最少步解:布局A的所有解中满足步数为最少步解的步数的布局,称为最少步解;
性质1:布局的解可能是空集;
性质2:最少步解属于解的子集,满足(最少步解的个数) ≤ (解的个数);
层级关系
层模型
表述:存在一起始布局A,从它开始衍生出有限个布局,每个布局抽象为一个节点,同时称A为根节点;由于任一由A衍生出布局到根节点存在一个确定的最少步数,将其称之为到根节点的距离;将所有距离相同的布局称为一个层,层内元素无序且互异,根节点所在层称为第0层,之后依次排列可得有限个层;记排列的最后一层为第n层,则共有n + 1个层(包括第0层);
性质1:所有层中的元素集合即为根节点所在的群;
性质2:第a层节点的子布局必定在第a - 1层,第a层或第a + 1层,其中a满足1 ≤ a ≤ (n - 1);第0层的子布局必定在第1层;第n层的子布局必定在第n - 1层或第n层;
层间联系:若第a + 1层中存在第a层的子布局,则将两者链接起来,其中a满足0 ≤ a ≤ (n - 1);
向后传播:在第a层存在一节点K,在第a + 1层取得其子布局K'(0个及以上),再将每个K'在第a + 2层取得K''(0个及以上),以此类推得到分层的有限个布局,这个过程称为向后传播;
向前查找:在第a层存在一节点J,在第a - 1层取得其子布局J'(1个及以上),再将每个J'在第a - 2层取得J''(1个及以上),以此类推直到第0层的根节点,查找的数据即为节点J到根节点的全部最短路径合集,这个过程称为向前查找;
各参数在层模型中的体现
最少步数:某一节点所在层数为其到根节点的最少步数;
最短路径:对某一节点做向前查找,即可得到最短路径的合集;
最远步数:若共有n + 1层,则最远步数为n;
最远布局:最后一层的全部节点均为最远布局;
下方特征S的定义与上文一致,且下列讨论均为根节点有解的情况
最少步解的步数:第一次出现满足特征S的节点所在层数;
最少步解:在层数为最少步解的步数的层中,全部满足特征S的节点;
解
定义1:对满足特征S的节点向前查找,若得到的结果不存在任何满足特征S的节点,则该节点称为根节点的解;
定义2:对全部最少步解进行向后传播,将得到的结果进行标记;再向后逐层查找,若有满足特征S且未被标记的节点记为解,并进行向后传播,以此类推直到最后一层;整个过程得到的解与最少步解的集合称为根节点的解;
网模型
表述:网模型针对一个群,群中每一个布局称为节点,将每个节点与其子布局节点连接起来,整个群即可连成一个网状模型;
性质1:可在网模型中抽象出层模型及其层间连接;
性质2:层模型的节点等同于网模型,但节点间的连接是网模型的一个子集;
应用:选定网模型中的一个节点,可据此直接构建出该节点对应得层模型;